Here is an equation for a circle \(x^2y^24x6y3=0\) If we want to find the center and radius of the circle, we can rewrite the equation in the form \((xh)^2(yk)^2=r^2\) Start by rearranging the terms in the equation to make it easier to work with Group terms that include the same variable and move the 3 to the right side of the equationCho đường tròn C có phương trình x 2 y 2 – 4x 8y – 5 = 0 a, Tìm tọa độ tâm và bán kính của b, Viết phương trình tiếp tuyến với đi qua điểm A(1; Correct answers 2 question Which equation represents the general form a circle with a center at (–2, –3) and a diameter of 8 units?
Circles Circles Ellipse Quiz March 9 Midterm March 11 Next Thursday Ppt Download
The equation of the chord of the circle x^2+y^2-4x+6y+3=0
The equation of the chord of the circle x^2+y^2-4x+6y+3=0-Find the equation of the circle concentric with x^2 y^2 – 4x – 6y – 3 = 0 and which touches the y axis asked 22 hours ago in Circles by Daakshya01 (2k points) circles;Salah satu persamaan garis singgung lingkaran x 2 y 2 2x − 6y − 10 = 0 yang tegak lurus garis x 2y 1 = 0 adalah answer choices y = 2x − 14



Find The Points Of Intersections Of X2 Y2 2x 4y 1 Gauthmath
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the equation of the radical axis of circles `x^2y^2xy2=0` and `3x^23y x 2 2x x 2 = 0 x(x 2) 1(x2) = 0 x2 = 0 and x1 = 0 x = 2 and x = 1 There are two solutions to the quadratic equation x = 2, and x = 1 Substituting each of these solutions into either of the two original functions (the linear one would be easier) leads us to the corresponding y values y = x 3 For x = 2 then y = 2 3Calculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculo
Matemáticas / Geometría y Medida El siguiente logotipo lleva en su centro una circunferencia que cumple con la ecuación x 2 y 2 4x 6y 3 = 0 Determinar el radio del logotipo likes likes x^2 y^2 – 4x – 6y – 12 = 0, x^2 y^2 6x 18y 26 = 0 find the relative position of the pair of circles asked in Mathematics by Abhilasha01 ( 376k points) class11The ellipse E 1 \(\frac{x^{2}}{9}\frac{y^{2}}{4}\) = 1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes Another ellipse E 2 passing
The number of common tangents that can be drawn to the circle x 2 y 2 – 4x – 6y – 3 = 0 and x 2 y 2 2x 2y 1 = 0 is (A) 1 (B) 2 3 (D) 4 24 The equation of the circumcircle of the triangle formed by the lines y 3x 6, y 3x 6 = = and y = 0 is (A) x 2 y 2 – 4y = 0 (B) x 2 y 2 4x = 0 x 2 y 2 – 4y = 12 (D) x 2Graph x^2y^24x6y3=0 x2 y2 4x − 6y − 3 = 0 x 2 y 2 4 x 6 y 3 = 0 Add 3 3 to both sides of the equation x2 y2 4x−6y = 3 x 2 y 2 4 x 6 y = 3 Complete the square for x2 4x x 2 4 x Tap for more steps Use the form a x 2 b x c a x 2Given {eq}2x^2 y^2 4x 6y 3 = 0 {/eq}, let's first reorder the terms and factor out a {eq}2{/eq} from the {eq}x{/eq}terms to get {eq}2(x^22




The Line Mx Y M 2 0 Meets The Circle X 2 Y 2 4x 6y 3 0 At A And Bthe Lines Joining A And B To The Centre Meet The




Find The Centre Ans Radius Of Each Of The Following Circles X 2 Y 2 4x 6y 5
The equation of chord of x^2y^24x6y3=0 whose mid point is(1,2)is Share with your friends Share 2`x^2y^24x6y3=0` আবিষ্কার `(dy)/(dx)` এ `(1, 6)` JEE Main 21 4th session starts from Aug 26, application last date extendedX^{2}y^{2}4x6y3=0 zs Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject Each new topic we learn has symbols and problems we have never seen The unknowing




Consider Two Circles X 2 Y 2 4x 6y 8 0 And X 2 Y 2 2x 3 0 Sta




2x22y2 4x6y 30 See How To Solve It At Qanda
If `x^2y^24x6y3=0`, then minimum possible value of the expression `16 1/(x2)^21/(y3)^2` is equal to Step by step solution by experts to help you in doubt clearance & scoring excellent marks in examsFind the equation of the circle concentric with x 2 y 2 − 4x − 6y − 3 = 0 and which touches the yaxis Advertisement Remove all ads Solution Show Solution Since, the circles are concentric \\Rightarrow\ Centre of required circle = Centre of x 2 y 2 − 4x − 6y − 3 = 0X^2 y^2 4x 6y 36 = 0 We will use completing the square method to rewrite the equation into the form (xa)^2 (yb)^2 = r^2 where (a,b) is the center and r is the radius Let us rewrite




Diketahui Persamaan Lingkaran X Y 4x 6y 3 0 Tentukan Pusat Dan Jari Jari Nya Mohon Brainly Co Id




The Circle Concentric With X 2 Y 2 4x 6y 3 0 And Radius
4 x^2 y^2 8x 7 = 0 5 x^2 y^2 4x 6y 3 = 0 Answer by ewatrrr() (Show Source) You can put this solution on YOUR website!X^2y^22x6y9=0 This problem has been solved! Equation of the circle is given as x 2 y 2 4x 6y 3 = 0 So changing it as standard equation, as (x h) 2 (y k) 2 = a 2, here ( h , k) are centre of the circle and a is the radius x 2 y 2 4x 6y 3 = 0 x 2 y 2 4x 6y = 3 Adding 4 and 9 on both sides we get, x 2 y 2 4x 4 6y 9 = 3 4 9 (x 2) 2 (y 3 ) 2 = 4 2 (i) So the centre is ( 2 ,3) and Radius




The Equation Of The Chord Of X 2 Y 2 4x 6y 3 0 Whose Mi




Encuentra La Ecuacion General De La Circunferencia Con Centro En C 2 3 Y Radio Igual A 4 Seleccione Brainly Lat
Find the equation of tangent for the circle through point (2,4) given that x 2 y 2 – 2x – 4y 1 = 0 5 Show that the point (7, 5) lies on the circle x 2 y 2 – 6x 4y – 12 = 0 Find the equation of tangent to the circle at the pointGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! The equation is x 2 y 2 4x 6y 3 = 0 Compare the above equation with Ax 2 Bxy Cy 2 Dx Ey F = 0 A = 1 and C = 1 Since, A and C have opposite signs The given equation represents the curve hyperbola Write the equation x 2 y 2 4x 6y 3 = 0 in standard form of hyperbola




1 Find The Equation Of The Circle Concentric X2 Y2 4x 6y 3 0 And Which Touches The Brainly In




X 2 Y 2 4x 6y 3 0 Find Dy Dx At 1 6
Write the equations as $$ (x3)^2y^2=5 $$ and $$ (x1)^2(y1)^2=10 $$ Thus, we have a triangle with sides $\sqrt{5}$, $\sqrt{10}$, $\sqrt{5}$ $\hspace{3cm}$ The Law of Cosines says $$ 5=5102\sqrt{5}\sqrt{10}\cos(\alpha) $$ which implies $$ \cos(\alpha)=\frac1{\sqrt2} $$ We could also recognize the $45{}45{}90$ triangleCâu hỏi Cho đường tròn có phương trình x 2 y 2 4x6y3=0 và đường thẳng Δ 3x – 4y – 2 = 0 Khẳng định nào sau đây là đúng?The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}4xy^ {2}6y3=0 x2 − 4x y2 − 6y 3 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 4 for b, and y^ {2}6y3 for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}




Let A 3 7 And B 6 5 Are Two Points C X 2 Y 2 4x 6y 3 0




Write The Equation Of The Circle Below In Standard Chegg Com
Question Complete The Square In Order To Put The Equations Into Standard Form 1 X^2 Y^2 2x 4y 11 =0 2 X^2 Y^2 4x 6y 3 = 0 3 X^2 Y^2 7x Y 1 = 0 4 4x^2 4y^2 16y 16 =00 votes 1 answer Find the equation of the circle concentric with the circle x^2 y^2 4x 6y 11 = 0 and passing through the point P(5, 4)X² y² 4x 6y 3 = 0 (x² 4x 4 4) (y² 6y 99) = 3 (x²4x 4) (y²6y9) = 349 (x2) ² (y3) ²=16 This is circle with center(2,3) and radius 4 Since required circle is concentric to this circle So its center will be (2,3) Let circle be (




How To Solve This Find The Equation To The Circle Concentric With The X 2 Y 2 4x 6y 3 0 And Which Touches The Y Axis Quora



1
The cordiantes, farthest from the origin on the circle, will lie on the line joining the centre of the circle and the point (0,0) Centre is (6,2) So eqn of the line is 3y=x Sub x=3y in the circle eqn, and solve for y You will get two values of y (corresponding to which you would get two values of x)0) c, Viết phương trình tiếp tuyến với vuông góc với đường thẳng 3x – 4y 5 = 0X^2y^2–4x6y3=0 (x2)^2(y3)^2=49–3=10=(10^1/2)^2 Centre(2,3) , radius =10^1/2 units Let y=mxc is the eqof tangent, put m=tan45°=1 y=xc




2 V 3 2 109 Or X2 Y2 4x 6y 96 0 X 2 2 Y 3 2 Fig 24 10 13 Fm Find The Equation Of The Circle Having Centre At 3 4 And Touching The Line Example 3 5x 12y 12 0 Insert Fxemplar
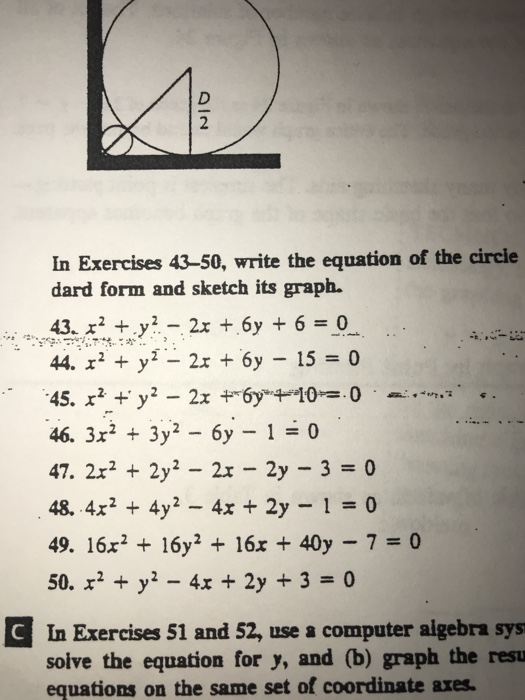



In Exercises 43 50 Write The Equation Of The Circie Chegg Com
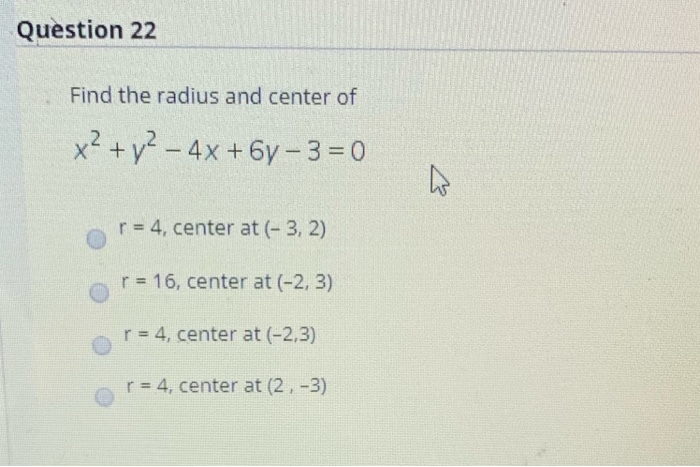
The number of common tangents that can be drawn to the circle x 2 y 2 – 4x – 6y – 3 = 0 and x 2 y 2 2x 2y 1 = 0 is (A) 1 (B) 2 3 (D) 4 38 A circle S of radius 'a' is the director circle of another circle S 1 S 1 is the director circle of circle S2 and so on If the sum of the radii of all these circles is 2, then the Explanation x2 4x y2 −6y − 3 = 0 or x2 4x 4 y2 −6y 9 = 4 9 3 or (x 2)2 (y −3)2 = 42 The centerradius form of the circle equation is (x– h)2 (y– k)2 = r2, with the center being at the point (h,k) or ( − 2,3) and the radius being r = 4 So, center is at ( − 2,3) and radius is 4 unit graph {x^24xy^26 y3Hi, Standard Form of an Equation of a Circle is where Pt(h,k) is the center and r is the radius 1 3 use above, substitute values given
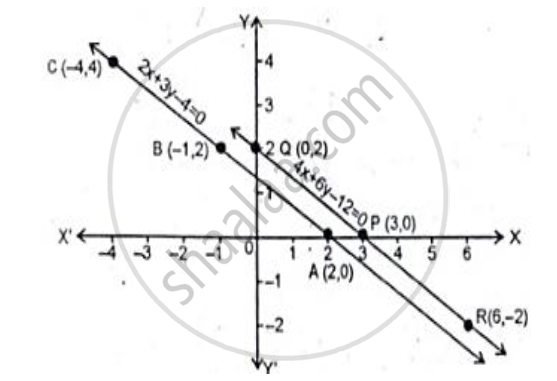



Show Graphically That The System Of Equations 2x 3y 4 4x 6y 12 Is Inconsistent Mathematics Shaalaa Com




Titik Pusat Dan Jari Jari Lingkaran Dengan Persamaan X2 Y2 4x 6y 3 0 Adalah Brainly Co Id
The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction y^ {2}4yx^ {2}3=0 y 2 − 4 y x 2 3 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 4 for b, and x^ {2}3 for c in the quadratic formula, \frac {The square of the length of the tangent from \( \Large \left(3,\ 4\right) \) to the circle \( \Large x^{2}y^{2}4x6y3=0 \) isThe equation of circle concentric with the circle x^2y^24x6y3=0 and touching y acis is 1 See answer pgracevolau5405 is waiting for your help Add your answer and earn points devanshchoudhary17mc devanshchoudhary17mc AnswerAll are from 10th cbse boards here Stepbystep explanation



Solve The Systems Of Equations Using Matrix Method 5x 7y 2 0 4x 6y 3 0 Sarthaks Econnect Largest Online Education Community




If X 2 Y 2 4x 6y 3 0 Then Minimum Possible Value Of The Expression 16 1 X 2 2 1 Y 3 2 Youtube
Rearrange into the standard form of the equation of a circle with centre (2, 3) and radius 5 >0 = x^2y^24x6y12 =(x^24x4)(y^26y9)25 =(x2)^2(y3)^25^2 Add 5^2 to both ends and transpose to get (x2)^2(y(3))^2 = 5^2 This is in the form (xh)^2(yk)^2 = r^2 the standard form of the equation of a circle with centre (h, k) = (2, 3) and radius r=5 graph{(x^2y^24x6y12)((x2 高一数学 圆的一般式方程 x平方y平方4x6y3=0 1 x^2y^22x-2y-2=0和x^2y^2-4x-6 3 方程x^2y^24x6y13=0的解集 13A) x^2y^24x6y51=0 b) x^2y^24x6y51=0 c) x^2y^24x6y3=0 d) x^2y^24x6y3=0



How Would You Show That Circles X2 Y2 4x 6y 12 0 And X2 Y2 6x 18y 26 0 Touch Each Other What Is The Point Of Contact And Their Common Tangent Quora




Find The Angle Between The Circles X 2 Y 2 12x 6y 41 0 And X 2 Y 2 4x 6y 59 0
Click here👆to get an answer to your question ️ Find the equation of the circle concentric with x^2 y^2 4x 6y 3 = 0 and which touches the y axis La ecuación x^2y^24x6y3=0 representa en el plano R2 a) un punto con coordenadas (2,3) b) una circuferenc Recibe ahora mismo las respuestas que necesitas!If the area of the circle 4 x 2 4 y 2 8 x − 1 6 y λ = 0 is 9 π sq units, then the value of λ is View solution If s , s 1 , s 2 be the circles of radii 5,3,2 respectivelyIf s 1 a n d s 2 touch externally and they touch internally with S



The Number Of Common Tangents To The Circles X 2 Y 2 4x 6y 12 0 Sarthaks Econnect Largest Online Education Community




Find The Angle Between The Circles X 2 Y 2 4x 6y 3 And X 2 Y 2 8x 4y 11 0 Brainly In
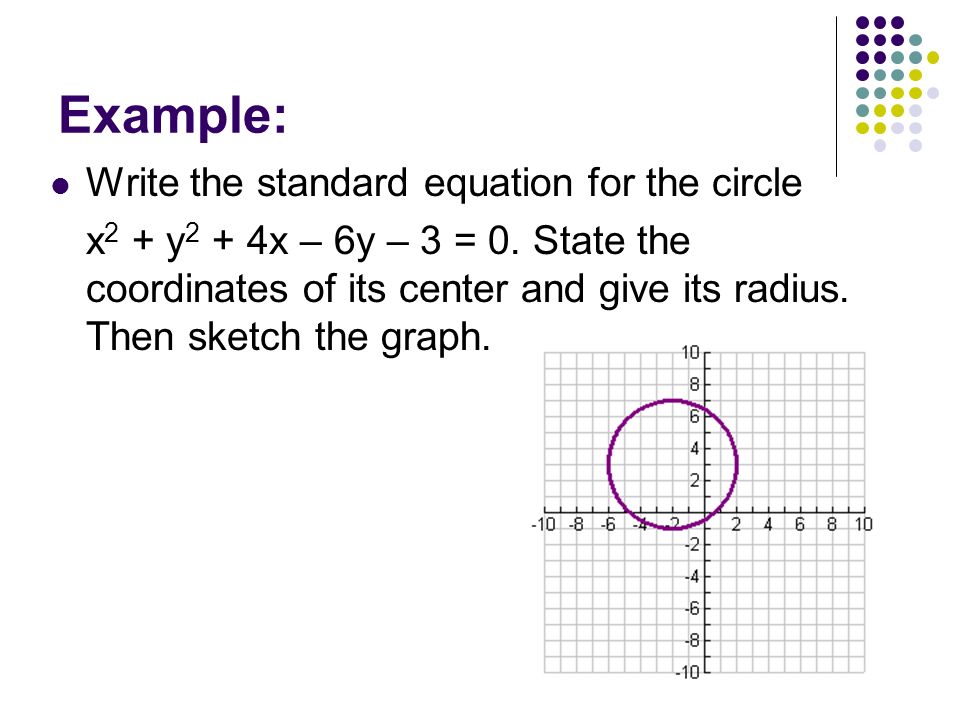
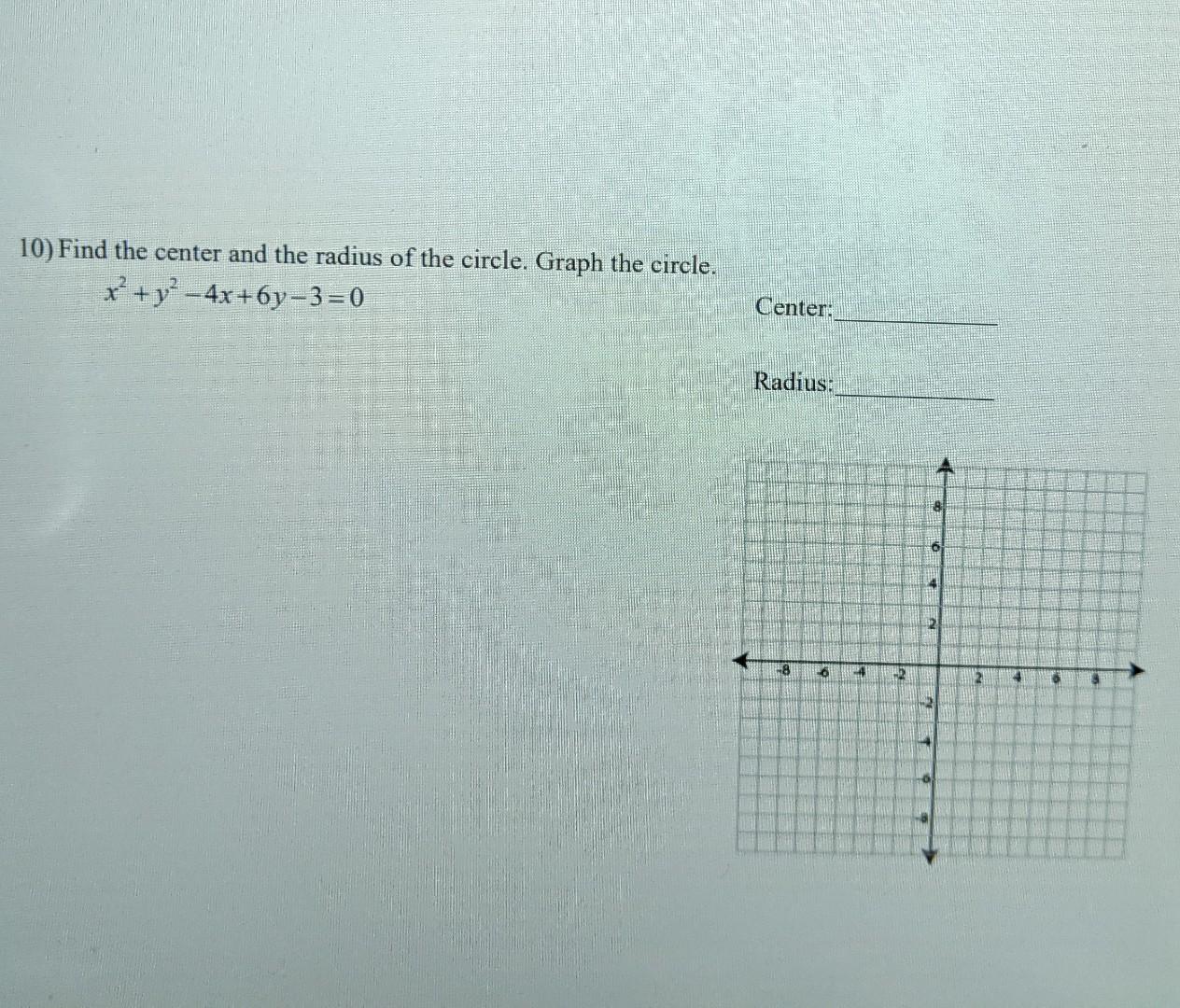
Find the roots of the equation y = x2 – 4x 2 by completing the square 6 Write the equation of the circle in centerradius form x 2 y 2 – 4x 6y – 3 = 0Solution for X^2y^24x6y3=0 equation Simplifying X 2 y 2 4x 6y 3 = 0 Reorder the terms 3 X 2 4x 6y y 2 = 0 Solving 3 X 2 4x 6y y 2 = 0 Solving for variable 'X' Move all terms containing X to the left, all other terms to the right Add '3' to each side of the equation 3 X 2 4x 6y 3 y 2 = 0 3 Reorder the terms 3 3 X 2 4x 6y y 2See the answer Find the center and the radius of the circle x^2y^22x6y9=0 Expert Answer Previous question Next question Get more help from Chegg Solve it with our precalculus problem solver and calculator




The Straight Line X Y 3 0 Touches The Circle X2 Y2 4x 6y 11 0 At The Point Whose Coordinates Are




X2 Y2 4x 6y 3 0 Gauthmath
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW For the circles `S_1 x^2 y^24x6y12 = 0` and `S_2 x^2 y^2 6x 4y12=Precalculus Find the Center and Radius x^2y^24x6y3=0 x2 y2 − 4x − 6y − 3 = 0 x 2 y 2 4 x 6 y 3 = 0 Add 3 3 to both sides of the equation x2 y2 −4x−6y = 3 x 2 y 2 4 x 6 y = 3 Complete the square for x2 −4x x 2 4 x Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a{eq}\displaystyle x^2 y^2 4x 6y 3 = 0 {/eq} Standard Equation of a Circle Geometrically, a circle is a {eq}2 {/eq}dimensional planner geometry shape that has a



The Number Of Common Tangents To The Circles X 2 Y 2 4x 6y 12 0 Sarthaks Econnect Largest Online Education Community




Prove That The Circle X 2 Y 2 2x 2y 1 0 And Circle X 2 Y
The equation of the common chord of the circles x 2 y 24x4y = 0 and x 2 y 2 = 16 is xy = 4 which meets the circle x 2 y 2 = 16 at points A(4,0) and B(0,4) Obviously OA ^ OB Hence the common chord AB makes a right angle at the centre of the circle x 2 y 2 = 16 Hence (D) is the correct answer Q12 The number of common tangents that can




7 F A F X2y22x2y10 See How To Solve It At Qanda




Find The Points Of Intersections Of X2 Y2 2x 4y 1 Gauthmath
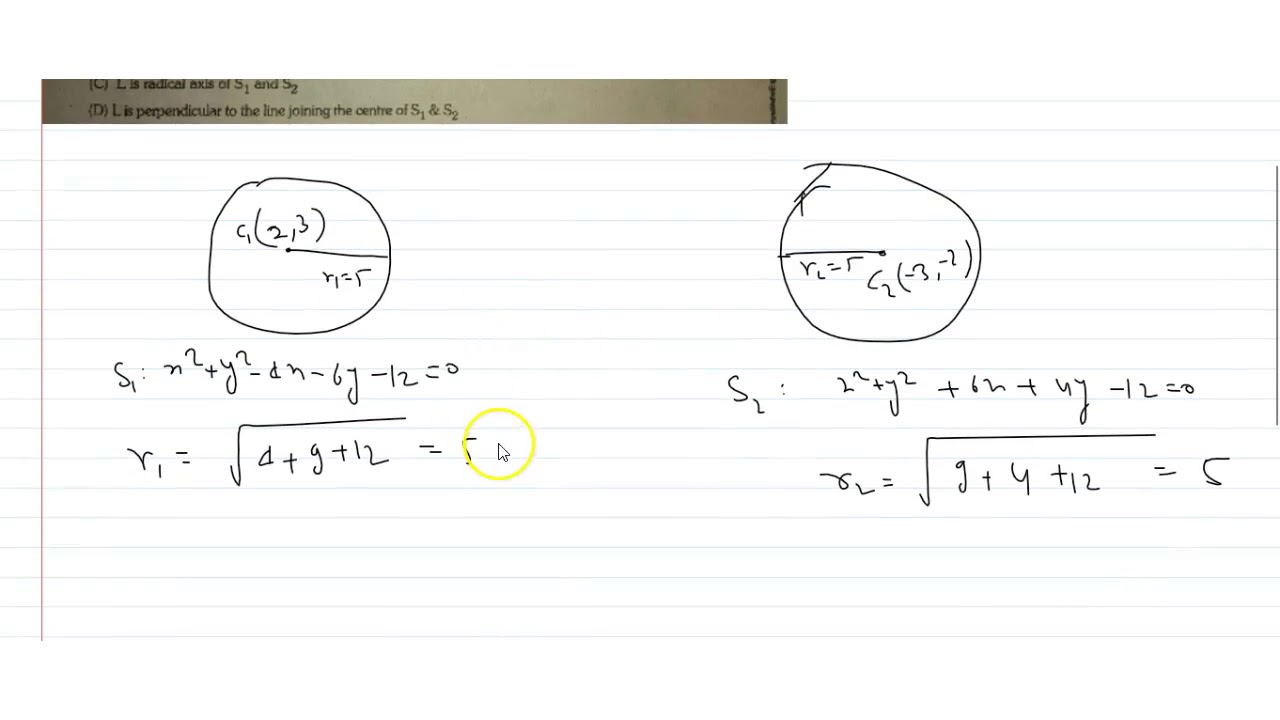



For The Circles S 1 X 2 Y 2 4x 6y 12 0 And S 2 X 2 Y 2 6x 4y 12 0 And The Lin Youtube




Solution A Circle Whose Equation Is X 2 Y 2 4x



How To Find The Radius Of The Circle X Y 4x 6y 12 0 Quora




Nally 29 The Equation Ofthe C See How To Solve It At Qanda




X 2 Y 2 4x 6y 3 0 Find Dy Dx At 1 6 Youtube




Working With Circles



X2 Y2 4x 6y 3 0 Najti Radius Okruzhnosti Shkolnye Znaniya Com




X2 Y2 2x 4y 1 0 X2 Y2 4x 6y 3 0 Find The Points Of Gauthmath




The Equations Of The Three Circles Are X 2 Y 2 6x 6y 4 0 X 2 Y 2 2x 4y 3 0 And X 2 Y 2 2 Youtube




A Chord Of The Circle X 2 Y 2 4x 6y 0 Passing Through The Origin Subtends An Angle Ar Youtube



1




Solved 4 Write The Equation Of The Circle In The Form X Chegg Com




Area Of A Equi Triangle Inscribed In A Circle X2 Y2 4x 6y 3 0 Brainly In




Circles Circles Ellipse Quiz March 9 Midterm March 11 Next Thursday Ppt Download



What Is The Equation Of Tangent To The Circle X2 Y2 4x 6y 3 0 Which Makes A 45 Angle With X Axis Quora



How Would You Show That Circles X2 Y2 4x 6y 12 0 And X2 Y2 6x 18y 26 0 Touch Each Other What Is The Point Of Contact And Their Common Tangent Quora




Find The Equation Of The Circle Which Passes Through The Origin An




2find The Equation 0c The Ci See How To Solve It At Qanda




The Equation Of The Chord Of X2 Y2 4x 6y 3 0 Whose Mid Point Is 1 2 Isa X Y 1 0b 2x 3y




Find The Coordinates Of The Centre Of The Circlex 2 Y 2 4x 6y 3 Given That Point A Outside The Circle Has Coordinates A Maths Straight Lines Meritnation Com
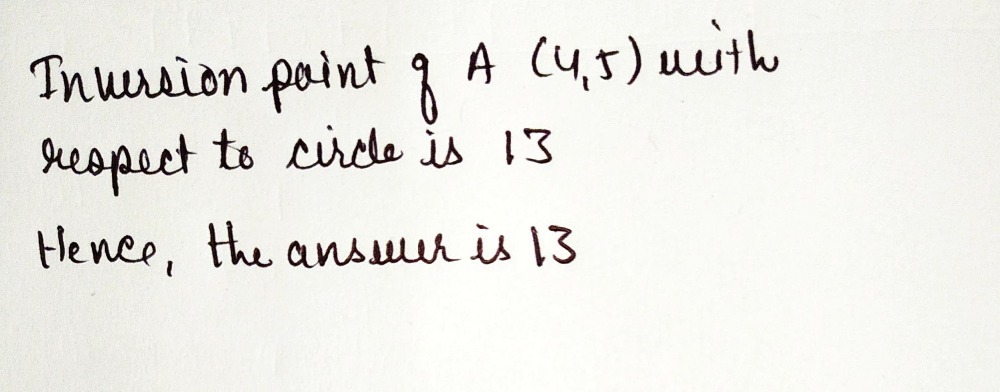



The Equation Of An Inversion Circle Is X2 Y2 4x 6y Gauthmath




Find The Equation Of The Circle Concentric With The Circle X 2 Y 2 4x 6y 11 0 And Passing Through The Point P 5 4




The Circle Concentric With X 2 Y 2 4x 6y 3 0 And Radius



Persamaan Bayangan Dari Lingkaran X2 Y2 4x 6y 3 0 Jika Dirotasikan 0 360derajat Adalah Brainly Co Id



Solved 10 Find The Center And The Radius Of The Circle Chegg Com



Circles X 2 Y 2 4x 6y 3 0 And 2 X 2 Y 2 6x 4y C 0 Cut At Right Angle If C Options A 18 B 16 C 14 D 12 Sarthaks Econnect Largest Online Education Community




Cho Hai đường Tron Co Phương Trinh C1 X 2 Y 2 4x 6y 3 0 Va C2 X 2 Y 2 2x 4y 1 0 Cac đường Thẳng Tiếp Xuc Với Cả Hai đường Tron Tren La



How To Solve This Find The Equation To The Circle Concentric With The X 2 Y 2 4x 6y 3 0 And Which Touches The Y Axis Quora



Solution Trying To Help My Son But It 39 S Been Waaaay Too Long Ago X 2 Y 2 4x 6y 3 0



How Would You Show That Circles X2 Y2 4x 6y 12 0 And X2 Y2 6x 18y 26 0 Touch Each Other What Is The Point Of Contact And Their Common Tangent Quora



1




Length Of Intercept Made By Line X Y 2 On The Circle X 2 Y 2 4x 6y 3 0 Is




Help Please Point Question Which Equation Represents The General Form A Circle With A Center Brainly Com



Question 22 Find The Radius And Center Of X2 Y2 Chegg Com



What Is The Equation Of Tangent To The Circle X2 Y2 4x 6y 3 0 Which Makes A 45 Angle With X Axis Quora




If X 2 Y 2 4x 6y 3 0 Then Minimum Possible Value Of The Express



What Will Be The Equation Of A Circle Concentric With The Circle Math X 2 Y 2 4x 6y 9 0 Math And Passing Through The Point Math 4 5 Math Quora
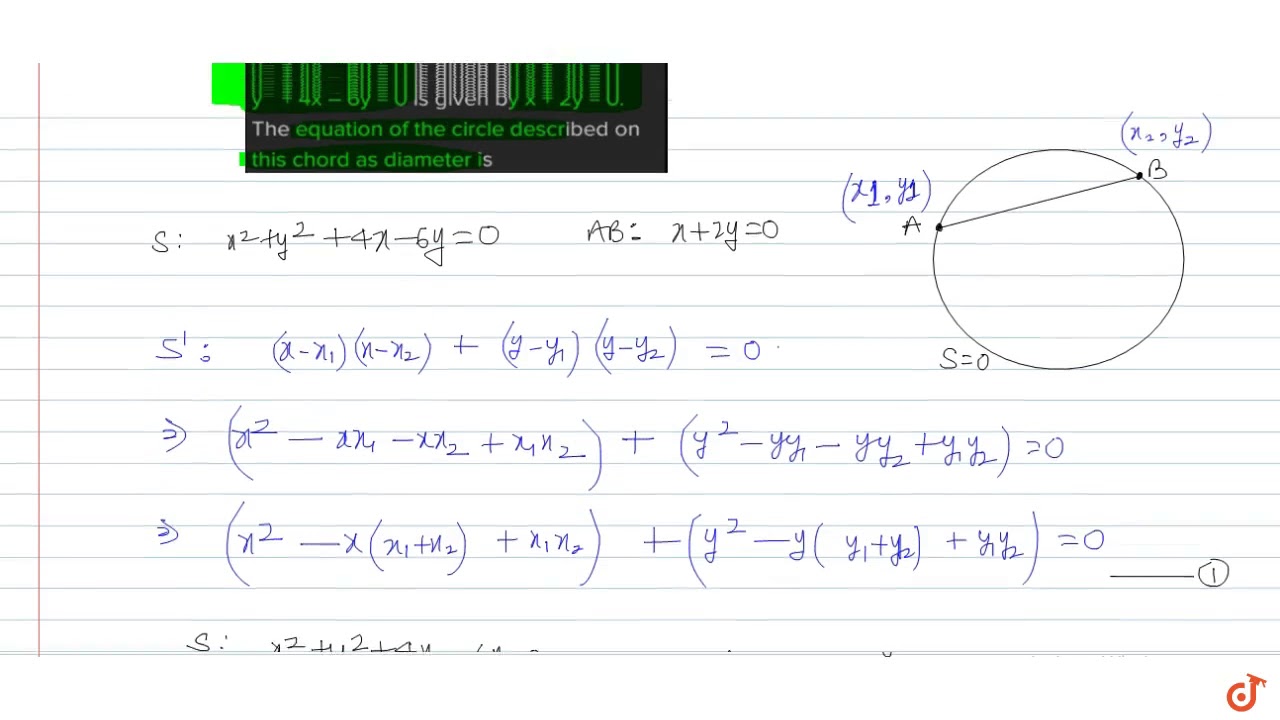



The Equation Of A Chord Of The Circle X 2 Y 2 4x 6y 0 Is Given By X 2y 0 The Equ Youtube




Solved 7 Find The Radius And The Coordinates Of The Cent Chegg Com



Q Tbn And9gcrdhoagwo Onfar8vymphdsbmkccjdbftwi Qp7bcfxjnakjpgc Usqp Cau




Panjang Jari Jari Lingkaran X 2 Y 2 4x 6y 3 0x 2 Y 2 4x 6y 3 0 Adalah Satuan Brainly Co Id




The Circle Concentric With X 2 Y 2 4x 6y 3 0 And Radius




X 2 Y 2 4x 6y 3 0 Novocom Top




Given The Equation Of A Circle X2 Y2 4x 6y 3 0 Ii Gauthmath




Find The Equation Of The Circle Which Is Concentric With The Circl



The Intercept Made By The Circle X 2 Y 2 4x 6y 3 0 On The Line X Y 3 0 Isa Sqrt 14 B 2 Sqrt 14 C 6 Sqrt 2 D 3 Sqrt 2 Snapsolve




Solution A Circle Whose Equation Is X 2 Y 2 4x 6y 23 0 Has Its Center At




Find The Centre And Radius Of Each Of The Circles Whose Equat




Find The Locus Of The Foot Of The Perpendicular From The Origin To Chord Of The Circle X 2 Y 2 4x 6y 3 0 Which Subtend A Right Angle At The Origin




55 Ifa Circle Having Centreat See How To Solve It At Qanda




The Circle Concentric With X 2 Y 2 4x 6y 3 0 And Radius




For The Equation X2 4x 6y 3 0 Do The Following Chegg Com




Diberikan Lingkaran L X2 Y2 4x 6y 3 0 Dan Garis G 2x 3y 6 Mas Dayat




X2 Y2 4x 6y 3 0 Tentukan Pusat Dan Jari Jari Nya Brainly Co Id




Circles Page 156 Lingkaran Halaman Ppt Download



Www Topperlearning Com Answer Find The Equation Of The Circle Concentric With X2 Y2 4x 6y 3 0 And Which Touches The Y Axis Dtorlftt



What Is The Equation Of The Circle Concentric With X2 Y2 4x 6y 1 0 And Having A Radius Of 4 Units Quora




Please Answer This Question Q Consider Circles C1 X2 Y2 4x 6y Maths Conic Sections Meritnation Com



63 The Equation Of The Chord Ofx Y2 4x 6y 3 0 Whose Mid Point Is 7 1 2 Is1 X Y 1 02 Brainly In



X2 Y2 2x 4y 1 0 X2 Y2 4x 6y 3 0 Find The Points Of Gauthmath




Ppt Circles Powerpoint Presentation Free Download Id




8 Tu Uc Quuuuu X Y 8 0 9 Find The Equations Of The Tangents To The Circle R Y 2r 2y 3 0 Which Are Perpendicula 3x Y 4 0 10 Find The Equation Of The Tangents To The Circle X




5x 7y 2 0 4x 6y 3 0




X 2 Y 2 4x 6y 3 0 Novocom Top
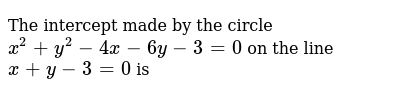



The Intercept Made By The Circle X 2 Y 2 4x 6y 3 0 On




The Intercept Made By The Circle X 2 Y 2 4x 6y 3 0 On




Answered C X Y 4x 6y 3 0 D X Y 4x 6y Bartleby




6 Find The Equation Of The Circle Which Cuts The Following Circles Orthogonally 2 3




Show That The Circles X 2 Y 2 2x 6y 12 0 And X 2 Y 2 6x 4




Show Graphically That The System Of Linear Equations 2x 3y 5 6y 4x 3 Youtube




Tentukan Persamaan Bayangan Dari Lingkaran X Y 4x 6y 3 0 Oleh Pencerminan Terhadap Sumbu X Brainly Co Id




5 Find The Equation Of The Ci See How To Solve It At Qanda




Panjang Jari Jari Lingkaran X Y 4x 6y 3 0 Adalah Brainly Co Id
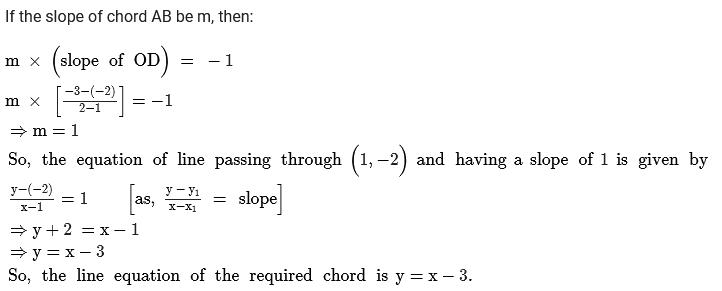



The Equation Of The Chord Of X2 Y2 4x 6y 3 0 Whose Mid Point Is 1 2 Isa X Y 1 0b 2x 3y



0 件のコメント:
コメントを投稿